Triangle calculator
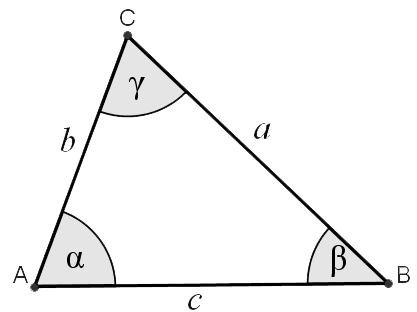
Solving Triangles Based on Known Properties
This triangle calculator is a tool designed to determine the unknown characteristics of a triangle when provided with a sufficient set of known properties. Triangles are defined by six primary characteristics: three sides (a, b, c) and three angles (α, β, γ). The goal of solving a triangle is to determine the unknown sides and angles based on the given information.
How It Works
The calculator requires three known properties to solve a triangle. These properties can be a combination of sides and angles, or derived properties such as area, perimeter, heights, or medians. The most common methods for solving triangles include:
- SSS (Side-Side-Side): When all three sides of the triangle are known, the calculator uses the Law of Cosines to determine the angles.
- SAS (Side-Angle-Side): When two sides and the included angle are known, the Law of Cosines is used to find the third side, followed by the Law of Sines to determine the remaining angles.
- ASA (Angle-Side-Angle): When two angles and the included side are known, the calculator uses the Law of Sines to find the remaining sides and the third angle.
- AAS (Angle-Angle-Side): When two angles and a non-included side are known, the calculator uses the Law of Sines to solve for the remaining sides and angle.
- SSA (Side-Side-Angle): When two sides and a non-included angle are known, the calculator may produce one or two possible solutions (the ambiguous case), depending on the given values.
Derived Properties
In addition to solving for sides and angles, the calculator can also determine derived properties such as:
- Area: Calculated using formulas like Area = 12 × b × c × sin α or Heron's formula.
- Perimeter: The sum of the three sides, a + b + c .
- Heights: The perpendicular distances from each vertex to the opposite side.
- Medians: The line segments from each vertex to the midpoint of the opposite side.
Practical Applications
Triangle calculators are widely used in fields such as engineering, architecture, physics, and computer graphics. They simplify complex calculations and ensure accuracy when working with geometric shapes.
Example
Suppose you know the lengths of two sides (a = 5, b = 7) and the included angle (γ = 45°). The calculator would:
1. Use the Law of Cosines to find the third side (c).
2. Use the Law of Sines to determine the remaining angles (α and β).
3. Optionally, calculate the area, perimeter, or other derived properties.
What Do the Symbols Mean in Triangle Calculations?
When working with triangles, specific symbols are used to represent the sides, angles, and other properties. Understanding these symbols is essential for solving triangle problems and using triangle calculators effectively. Below is a detailed explanation of the most commonly used symbols:Sides of the Triangle
Represent the lengths of the sides of the triangle. By convention:- a is the length of side BC (opposite angle A or α).
- b is the length of side AC (opposite angle B or β).
- c is the length of side AB (opposite angle C or γ).
Internal Angles
The internal angles of the triangle, by convention:- A or α is the angle at vertex A (opposite side a).
- B or β is the angle at vertex B (opposite side b).
- C or γ is the angle at vertex C (opposite side c).
Altitudes (Heights)
The altitudes (or heights) of the triangle are the perpendicular distances from each vertex to the opposite side:- ha is the altitude corresponding to side a (from vertex A to side BC).
- hb is the altitude corresponding to side b (from vertex B to side AC).
- hc is the altitude corresponding to side c (from vertex C to side AB).
Medians
The medians of the triangle are the line segments from each vertex to the midpoint of the opposite side:- ma is the median corresponding to side a (from vertex A to the midpoint of side BC).
- mb is the median corresponding to side b (from vertex B to the midpoint of side AC).
- mc is the median corresponding to side c (from vertex C to the midpoint of side AB).
Area
The symbol T represents the area of the triangle, which is the amount of space enclosed within its sides.Perimeter
The symbol p represents the perimeter of the triangle, which is the sum of the lengths of its sides.Semiperimeter
The symbol s represents the semiperimeter of the triangle, which is half of the perimeter.How Does This Calculator Solve a Triangle?
Solving a triangle involves determining its unknown sides, angles, and other properties based on the given information. The process typically occurs in two main phases:
Phase 1: Expert Phase – Determining the Three Sides
The first phase focuses on calculating the lengths of the three sides of the triangle using the entered data. This phase varies depending on the specific task and the type of input provided (e.g., sides, angles, area, or other properties). The calculator applies a knowledge base of geometric principles and relationships to iteratively solve for the unknown sides.Phase 2: Calculating Triangle Properties
Once the lengths of all three sides are known, the calculator proceeds to the second phase, where it computes the remaining properties of the triangle. By leveraging mathematical principles and logical reasoning, the calculator provides accurate and comprehensive solutions for a wide range of triangle problems.Examples of how to enter a triangle:
a=3 b=4 c=5 ... triangle calc by three sides a,b,c.
B=45 c=10 a=9 ... triangle calc by two sides a,c and included angle B.
A=25 C=80 b=22
A=35 C=26 a=10
a=3 C=90 c=5 ... how to enter right-angled triangle.
a=3 β=25 γ=45 ... triangle calc if we know the side and two angles.
a=3 β=25 T=12 ... triangle calc, if know side, angle, and area of a triangle.
T=2.5 c=2 b=4 ... find side a if we know sides b, c, and the area of triangle T.
ma=1 b=2.5 c=2 ... calculation of the triangle if we know one median and any two sides.
ma=1 mb=2.5 mc=2 ... triangle calc by three medians.
ha=220, hb=165 hc=132 ... triangle calc by three heights.
a=7 β=40 mc=5 ... triangle calc by one side, one angle, and one median.
a:b:c=2:3:4 T=2.5 ... a triangle where the known side ratio and its area.
A:B:C=1:4:5 a=2 ... calculating triangle if we know the ratio of the internal angles and one side.
B=45 c=10 a=9 ... triangle calc by two sides a,c and included angle B.
A=25 C=80 b=22
A=35 C=26 a=10
a=3 C=90 c=5 ... how to enter right-angled triangle.
a=3 β=25 γ=45 ... triangle calc if we know the side and two angles.
a=3 β=25 T=12 ... triangle calc, if know side, angle, and area of a triangle.
T=2.5 c=2 b=4 ... find side a if we know sides b, c, and the area of triangle T.
ma=1 b=2.5 c=2 ... calculation of the triangle if we know one median and any two sides.
ma=1 mb=2.5 mc=2 ... triangle calc by three medians.
ha=220, hb=165 hc=132 ... triangle calc by three heights.
a=7 β=40 mc=5 ... triangle calc by one side, one angle, and one median.
a:b:c=2:3:4 T=2.5 ... a triangle where the known side ratio and its area.
A:B:C=1:4:5 a=2 ... calculating triangle if we know the ratio of the internal angles and one side.
Triangles in word problems:
- Triangle - ratio
Change the triangle in a ratio of 3:4 The length of the sides of a triangle: a = 7 cm b = 6 cm c = 5 cm - Triangle - angles
ABC triangle, alpha = 54 degrees 32 minutes, beta = 79 degrees. What are the sizes of the exterior angles? - A triangle 10
A triangle has vertices at (4, 5), (-3, 2), and (-2, 5). What are the coordinates of the vertices of the image after the translation (x, y) arrow-right (x + 3, y - 5)? - Triangular flowerbed
A gardener plants one row of tulips around a triangular bed with sides of 5 m, 6 m, and 10 m. How many tulip bulbs does he need if he wants to plant 8 bulbs on a length of 1 m?
- The sides 7
The sides of the triangle are 5.2, 4.6, and x. If the PERIMETER of the triangle is 11.2 feet, what is the length of the unknown side? (hint: draw a picture) - An isosceles 2
An isosceles triangular frame has a measure of 72 meters on its legs and 18 meters on its base. Find the perimeter of the frame. - Triangle and axes
Draw any triangle. Make the axis of its two sides. Their intersection is point S. (a) Measure the distance of point S from all three vertices (b) Draw the axis of the third side. - Sss triangle 2
Construct triangle ABC in which |AB|=5cm, |AC|=6cm and |BC|=9cm - Calculate
Calculate the area of the ABE triangle AB = 38mm and height E = 42mm Ps: please try a quick calculation
- The triangles
The triangles ABC and A'B'C 'are similar, with a similarity coefficient of 2. The angles of the triangle ABC are alpha = 35° and beta = 48°. Determine the magnitudes of all angles of triangle A'B'C '. - Approximation of tangent fx
What is the nontrigonometric formula (not a polynomial fit) for the growth curve that solves algebraically for the increase between tan(1 degree) and tan(2 degrees) continuing up to the tangent(45 degrees)? Okay, to use pi Check calculation for 12°. - Triangle 16953
In the ABC triangle, the alpha angle is 36 degrees. The beta angle is twice the gamma. What is this triangle? - A-shaped ladder
An unfolded double ladder (A-shaped rung) is 10 m long. How high will it reach if the painter extends both parts of the ladder and ensures that the two parts of the ladder are 12 m apart on the ground? - Identical 32703
How many identical triangles do the middle bars divide the triangle ▲?
A display of cans on a grocery shelf consists of 28 cans at the bottom, 25 cans in the next row, and so on. There are nine rows on a shelf. How many cans are there in the 9th row? How many cans are on display in total?more triangle problems »
Look also at our friend's collection of math problems and questions:
- triangle
- right triangle
- Heron's formula
- The Law of Sines
- The Law of Cosines
- Pythagorean theorem
- triangle inequality
- similarity of triangles
- The right triangle altitude theorem
